Het spectrum van waterstof
Sterren staan zo onbereikbaar ver weg
Sterren hebben tenminste één zaak gemeen: het zijn allemaal objecten die zeer ver van ons verwijderd zijn. Hun afstand is zo groot dat wij ze nooit zullen kunnen bereiken. De bijzonderste en quasi enige informatie die wij over sterren kunnen verkrijgen is afkomstig van het licht dat zij uitstralen. Niet te verwonderen dat astronomen voor dit sterrenlicht steeds een heel bijzondere aandacht hebben gekoesterd. Door de eeuwen heen werd het in al zijn componenten grondig bestudeerd. Indien we het licht van een ster door een prisma sturen toont het zich als een kleurenspectrum.
Spectroscopie
Ook onze Zon is een ster en heeft dus, net als alle andere sterren, een lichtspectrum. Twee wetenschappers, Joseph von Fraunhofer en Anders Jonas Angström, deden bij de studie van dit lichtspectrum in het begin van de 19de eeuw wel een zeer belangrijke ontdekking. Zij vonden dat er in het spectrum van de Zon bij bepaalde golflengten donkere lijnen aanwezig zijn (zie figuur 1). Het zijn de absorptielijnen zoals wij die vandaag nog kunnen observeren met onze heliostaat op MIRA. Deze ontdekking was de aanzet tot een fundamentele ontwikkeling in de astronomie, met name de spectroscopie. Aan de hand van de studie van sterspectra komt men ertoe om belangrijke eigenschappen van sterren te achterhalen, zoals hun chemische samenstelling, hun beweging aan de hemel of hun temperatuur.

Figuur 1
Copyright: MEES Solar Observatory
In het spectrum van de Zon vindt men steeds vier van deze absorptielijnen terug bij de volgende golflengten (λ):
656 nm, 486 nm, 434 nm en 410 nm waarbij 1 nm (nanometer) = 10-9 m.
Deze lijnen zijn specifiek voor het element waterstof. Ze wijzen dus ook op de aanwezigheid van waterstof in de Zon.
Om een verklaring te vinden voor het bestaan van deze lijnen moet men teruggrijpen naar de aard van de kleinste deeltjes in de natuur, de atomen. Deze deeltjes werden lang beschouwd als een soort mini-zonnestelsels waarbij een of meer elektronen rond een atoomkern draaiden.
Maar sinds de ontdekking van de kwantumtheorie aan het begin van de 20ste eeuw is dit beeld wel voorbijgestreefd. Volgens de kwantumtheorie draaien elektronen niet zoals in een mini-zonnestelsel rond de kern. Over de elektronen van een atoom kan men enkel beweren dat ze zich met een zekere waarschijnlijkheid op een of ander energieniveau rond de atoomkern bevinden. De fysische realiteit binnen het atoom kan men dus maar benaderen met een zekere waarschijnlijkheid.
Het element waterstof
In wat nu volgt gaan we verder enkel in op het element waterstof. Waterstof is qua materie het meest voorkomende bestanddeel van het heelal en speelt dan ook een zeer belangrijke rol in de astronomie. Het is ook het eenvoudigste element om te bestuderen, het bestaat immers alleen uit een atoomkern (= één proton) en één elektron.
Nu kan dit elektron, net als bij andere elementen, verspringen tussen verschillende energieniveaus die rond de atoomkern bepaald zijn. In figuur 2 worden de bijzonderste energieniveaus weergegeven. Ze worden meestal aangeduid met de letter n. Het niveau n = 1 duidt het niveau aan dat het dichtst bij de kern ligt, dan volgen al naargelang van de afstand tot de kern n = 2, n = 3, …
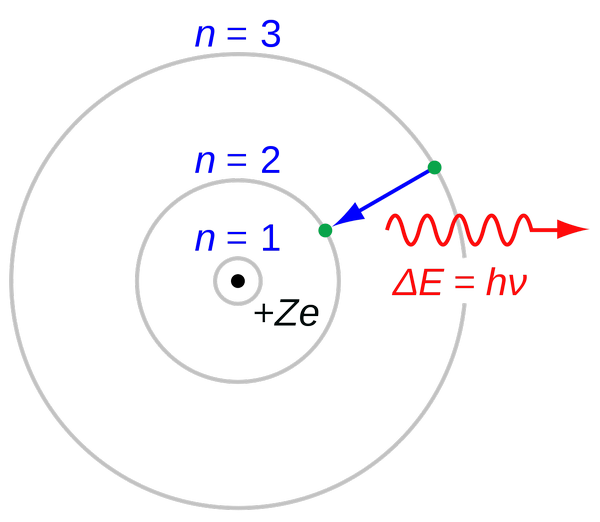
Figuur 2
Copyright: JabberWok @ English Wikipedia
Elk niveau heeft een bepaalde energiewaarde, en telkens het elektron van een bepaald niveau naar een ander niveau verspringt, zal er een corresponderende hoeveelheid energie ofwel vrijgegeven worden ofwel opgeslorpt worden.
In het eerste geval, wanneer energie wordt vrijgegeven, komt deze vrij onder de vorm van een min of meer energierijk foton. Er verschijnt dan in het spectrum een emissielijn waarvan de golflengte overeenstemt met het energieverschil tussen de betrokken niveaus. Dit is het geval telkens het elektron van een hoger niveau naar een lager niveau verspringt.
In het tweede geval, wanneer het elektron van een lager niveau naar een hoger niveau verspringt, vertoont het spectrum dan, volgens dezelfde regels, een absorptielijn. Het zijn deze lijnen die in figuur 1 zijn afgebeeld.
Orde in de chaos
De bekomen golflengten die men voor het element waterstof in het zichtbaar spectrum van de Zon terugvindt, komen op het eerste gezicht nogal chaotisch over. Ook Johann Balmer (1825-1898), een Zwitsers onderwijzer, dacht er hetzelfde over, en in zijn vrije tijd zocht hij of er in die getallen enige regelmaat terug te vinden was. Kon men een verklaring vinden voor deze waarden? Zat er in die waarden van resp. 656,3 - 486,1 - 434,0 en 410,2 nm een systematiek?
Uiteindelijk lukte het Balmer in 1885 om een formule te vinden, waarmee hij al deze waarden netjes kon terugvinden. Deze formule, bekend als de formule van Balmer, zie er als volgt uit:
1/λ = R . (1/22 - 1/n2)
waarin :
- R = 1,097 . 107 m-1. R wordt de constante van Rydberg genoemd.
- n = een parameter die verschillende waarden kan aannemen groter dan 2. De parameter n kan dus de waarden 3, 4, 5 of 6 aannemen.
Zo bekomt men bv. voor n=3:
1/λ = 1,097. 107 (1/22 - 1/33)
Of
λ = 656,3 nm (zie figuur 1)
Wat opvalt in de formule van Balmer is dat 2 er een speciale rol speelt. Zo moet men er voor de waarde n getallen nemen die groter zijn dan 2 (n>2). Maar als men aandachtiger kijkt, ziet men dat in de formule die Balmer uitwerkte enkel overgangen worden weergegeven die vanuit het 2de energieniveau vertrekken. Maar hoe zit het met de andere energieniveaus?
Verschillende reeksen spectraallijnen
Nu bevat het volledige zonnespectrum nog tal van andere spectraallijnen (figuur 3). En die beperken zich niet tot het zichtbaar gedeelte van het spectrum. Men vindt ook spectraallijnen terug in het infrarood en in het ultraviolet gebied van het spectrum. Deze absorptielijnen kan men helaas niet terugvinden met de formule van Balmer.
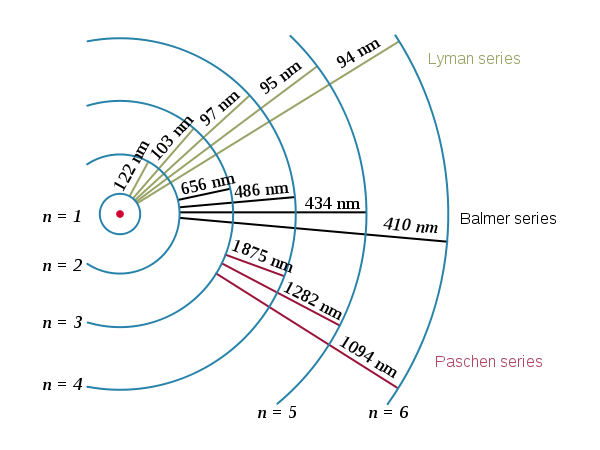
Figuur 3
Copyright: Szdori via Wikipedia
Het was de Zweed Johannes Rydberg (1854-1919) die in 1888 een meer algemene formule uitwerkte waarmee men alle spectraallijnen van waterstof kan terugvinden. Deze formule ziet er als volgt uit:
1/λ = R . (1/m2 - 1/n2)
waarin:
- R = de constante van Rydberg.
- m kan de waarden 1,2,3,… aannemen.
- n = een geheel getal dat groter is dan m (n>m)
Bij elke waarde m hoort dus een reeks van verschillende waarden van n en elkeen van die waarden van n blijkt overeen te komen met een bepaalde absorptielijn.
Voor m = 1 kan nde waarden 2, 3, 4,… aannemen. Men bekomt dan een reeks spectraallijnen die in het begin van de 20ste eeuw door T. Lyman werden ontdekt. Het is de Lymanreeks. Deze lijnen bevinden zich in het ultraviolet gedeelte van het spectrum. Men bekomt o.a. waarden als 121,57; 102,57; …
Voor m = 2 vindt men uiteraard de oorspronkelijke Balmerreeks terug. Zoals boven reeds aangegeven geeft m = 2 gewoon het tweede energieniveau weer.
Voor m = 3 komt men op volledig analoge manier uit bij een andere reeks lijnen die de Paschenreeks wordt genoemd. Deze lijnen vindt men terug in het infrarood deel van het spectrum. Men bekomt met de formule de waarden 1875, 1282, …
Voor m = 4 wordt de reeks lijnen genoemd naar Brackett. Men bekomt hier waarden als 405, 2625, …..
Voor m = resp. 5 en 6 verkrijgt men de Pfund- en de Humphreys-reeksen.
Al deze waarden hebben wel één belangrijke zaak gemeen: alle vertegenwoordigen ze energiesprongen van het elektron tussen de verschillende energieniveaus die eigen zijn aan waterstof. Samen vormen ze als het ware de barcode van het element waterstof.
Ook bruikbaar voor andere elementen
De formule van Rydberg werd op haar beurt nog veralgemeend. Wanneer men energiesprongen wil bestuderen van andere atomen dan waterstof, wordt de veralgemeende formule van Rydberg:
1/λ = Z2.R . (1/m2 - 1/n2)
waarin Z het atoomnummer van het atoom voorstelt.
In de tot nu toe gebruikte formule van Rydberg had Z uiteraard de waarde van 1. Deze laatste formule is wel enkel toepasselijk op geïoniseerde atomen die nog 1 elektron rond de atoomkern hebben. Dit is o.a. het geval bij He+ en Li2+. In andere gevallen moet men beroep doen op meer complexe methodes.
Tekst: Emile Beyens, februari 2018