Oneindig in wiskunde en sterrenkunde - deel 2

5. De ruimte wordt getemd door de meetkunde

Sinds Einstein in 1915 met zijn algemene relativiteitstheorie voor de dag kwam volstond de klassieke meetkunde van Euclides niet meer om toegang te verkrijgen tot een moderne visie op het heelal. In zijn visie was de ruimte niet langer star en onveranderlijk; de ruimte gedraagt zich daarentegen als een gekromd 'iets' en het is daarbij ook nog een veranderlijk 'iets'. De ruimte om ons heen krijgt een andere vorm door de aanwezigheid van een massa. Het is dus de massa van een voorwerp die de vorm van de ruimte bepaalt.

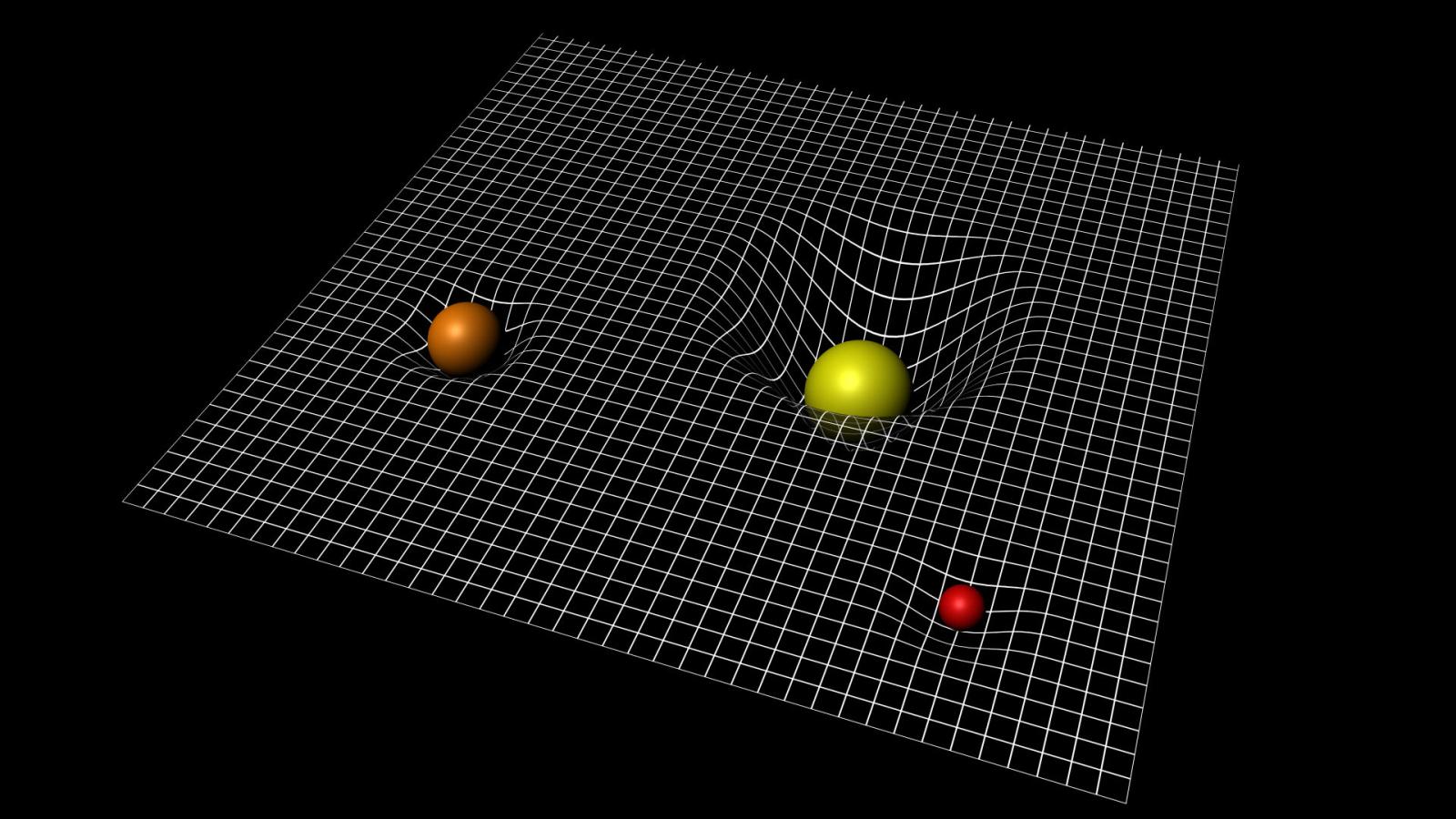
Copyright afbeelding: ESA Spacetime curvature

Sinds de relativiteitstheorie, met die nieuwe visie op de ruimte, is een meer complexe meetkunde nodig om een beter en dieper inzicht te verkrijgen in de structuur ervan, een meetkunde die niet enkel vlakke oppervlakten behandelt maar tevens oppervlakten die gebogen en vervormbaar zijn. 

Einstein had zich dit nieuw beeld van de ruimte gevormd dankzij zijn beroemde gedachte-experimenten, maar het is mede dankzij de inbreng van belangrijke wiskundigen dat het mogelijk werd om dit beeld van de ruimte een concrete inhoud te geven. Zij schiepen hiertoe het onontbeerlijke wiskundige instrument.

Tot die toonaangevende wiskundigen was er in de eerste plaats Bernard Riemann (1826-1866). Riemann was een zeer begaafd iemand die zowel op het gebied van de zuivere wiskunde als van de meetkunde grenzen heeft verlegd. Hij wordt beschouwd als de eerste grote moderne wiskundige. Op het gebied van de zuivere wiskunde is zijn naam verbonden aan de Riemann-hypothese, ook wel het Riemann-vermoeden genoemd. Het is een van de beroemdste problemen waarvoor nog steeds geen sluitend bewijs gevonden werd. Deze Riemann-hypothese is o.a. belangrijk bij het bestuderen van de verdeling van priemgetallen. Ook vandaag nog staat een aanzienlijke beloning van één miljoen dollar te wachten voor degene die een correct bewijs kan opstellen voor Riemanns hypothese...  

In het kader van dit artikel is echter vooral Riemanns werk over de meetkunde van belang. Hij stelde een meetkunde op die niet meer vanuit een driedimensionale ruimte moet benaderd worden, maar die ook gebruikt kan worden in een meerdimensionale gekromde ruimte, een meetkunde die toepasselijk is op positief gebogen oppervlakken. Andere belangrijke wiskundigen, zoals bijvoorbeeld Lobachevski en Bolyai, zouden Riemanns meetkunde verder uitwerken voor elliptische en hyperbolische ruimtes.

Copyright afbeelding: Wikipedia Publiek domein

In bovenstaande afbeelding wordt een beeld gegeven van die nieuwe meetkunde. Bovenaan rechts worden twee evenwijdige lijnen voorgesteld in een vlakke euclidische ruimte. In het midden wordt een boloppervlak voorgesteld voor een positief gebogen ruimte. Rechts onderaan zien we een open hyperbolische ruimte met een negatieve kromming. 

Deze meetkundige beschouwingen zijn van groot belang om de vorm en de toekomst van ons heelal te bepalen. Zal het heelal zich blijven uitzetten als een open heelal of zal het ooit opnieuw in elkaar krimpen als een gesloten heelal? Wat hier bepalend zal zijn is een kritische waarde voor de gemiddelde dichtheid, op grote schaal gemeten, van het heelal. 

6. De complexe vergelijking van Einstein

Het was de bedoeling van Einstein om, in het kader van zijn relativiteitstheorie, een algemene wiskundige formule op te stellen die zijn nieuwe visie op het heelal zou beschrijven. Maar Einstein was in de eerste plaats iemand met een zeer rijke verbeelding en geen superbegaafd wiskundige. En de wiskundige opdracht was in dit geval uiterst moeilijk. De verdere uitwerking van Einsteins formule zou tot stand komen dankzij de inbreng van zijn goede vriend en tevens begaafd wiskundige Marcel Grossmann (1878-1936). Helaas, het resultaat van deze ingewikkelde berekeningen bleek zo complex te zijn dat het in zijn algemene vorm onbruikbaar bleek te zijn. Zou Einsteins concept van het heelal dan een louter theoretische, onbewezen beschouwing blijven?

Gelukkig zouden anderen het over een andere boeg gooien. Zij zochten oplossingen voor Einsteins formule, maar maakten vooraf bepaalde veronderstellingen over het heelal. Zo men veronderstelde dat het heelal, op zeer grote schaal gezien, homogeen was en in alle richtingen gelijk, dan werd de formule van Einstein veel eenvoudiger. Het is op deze manier dat mensen als Aleksandr Friedmann (1888-1925), Karl Schwartzschild (1873-1916), Hermann Minkowski (1864-1909) en nog anderen ertoe gekomen zijn om de ruimtetijd concreet te beschrijven. Ook een beschrijving van die zo geheimzinnige zwarte gaten werd mogelijk. 

Ook de Belgische Georges Lemaître (1894-1966) hoort bij de bovengenoemde groep geleerden. Toen Edwin Hubble (1889-1953) in 1929 had vastgesteld dat sterrenstelsels zich van onze Melkweg verwijderden, zou Lemaître, gebruik makend van de relativiteitstheorie, hieruit afleiden dat het niet de sterrenstelsels waren die zich van ons verwijderden, maar dat het daarentegen het heelal zelf was dat zich uitzette. Verder beweerde Lemaître nog dat, aangezien het heelal zich nu uitzet, het vroeger noodzakelijk kleiner moet geweest zijn, dat het ooit een begin moet gehad hebben. Het is zijn befaamde 'Big Bang'. Zelf heeft Lemaître nooit over een Big Bang gesproken. Hij had het over een 'oer-atoom' dat aan de oorsprong lag van het heelal. 

Principe van de oerknal - Copyright afbeelding: Wikipedia Publiek domein

De eerste resultaten die Lemaître berekende voor de ouderdom van het heelal waren evenwel ver onder de realiteit. Hij schatte de ouderdom van het heelal op 4 miljard jaar. Op meer betrouwbare resultaten zou men nog enkele decennia moeten wachten. Recentere berekeningen ramen de ouderdom van het heelal op 13,7 miljard jaar. En Lemaître zou tot 1963 moeten wachten vooraleer zijn theorie algemeen aanvaard werd. 

Maar ook de zo revolutionaire relativiteitstheorie van Einstein heeft haar beperkingen. Het is een theorie die enkel kan gebruikt worden wanneer men het over de grote ruimte van het heelal heeft. Zij is toepasselijk op de studie van sterren, sterrenstelsels,... Bij het ontstaan van het heelal uit een oer-atoom was het heelal echter zeer klein, en in dit geval kan de relativiteitstheorie niet gebruikt worden. Als men het over kleine subatomaire deeltjes van de natuur heeft - wat het geval was bij het ontstaan van het heelal - moet men een beroep doen op de kwantumtheorie. Helaas, de relativiteitstheorie en de kwantumtheorie zijn twee theorieën die niet zomaar tegelijk kunnen gebruikt worden. 

Deze twee theorieën tot een sluitend geheel verenigen blijft ook vandaag nog steeds een belangrijk probleem. Zal voor dit probleem een nieuwe theorie, de snaartheorie, de oplossing bieden? De snaartheorie veronderstelt dat de kleinste deeltjes in de natuur eigenlijk geen deeltjes meer zijn, maar wel snaartjes. Het is een theorie die een beroep moet doen op zeer complexe, meerdimensionale wiskunde, waarover wiskundigen onderling het onder elkaar nog niet eens zijn. 

7. De ontbrekende massa-energie

In de tekst hierboven werd reeds gewezen op het belang van de gemiddelde massa-energiedichtheid van het heelal om er de vorm van te kunnen bepalen. Die gemiddelde dichtheid heeft men kunnen afleiden uit gedetailleerde foto's die de satellieten COBE, WMAP en Planck ons hebben bezorgd van de fossiele achtergrondstraling die door Penzias en Wilson werd ontdekt. Onderstaande foto werd genomen door de WMAP-satelliet en wijst op minieme temperatuurverschillen in het amper 380.000 jaar oude heelal. De meer donkere vlekken wijzen op warmere gebieden waar materie zich aan het vormen is. 

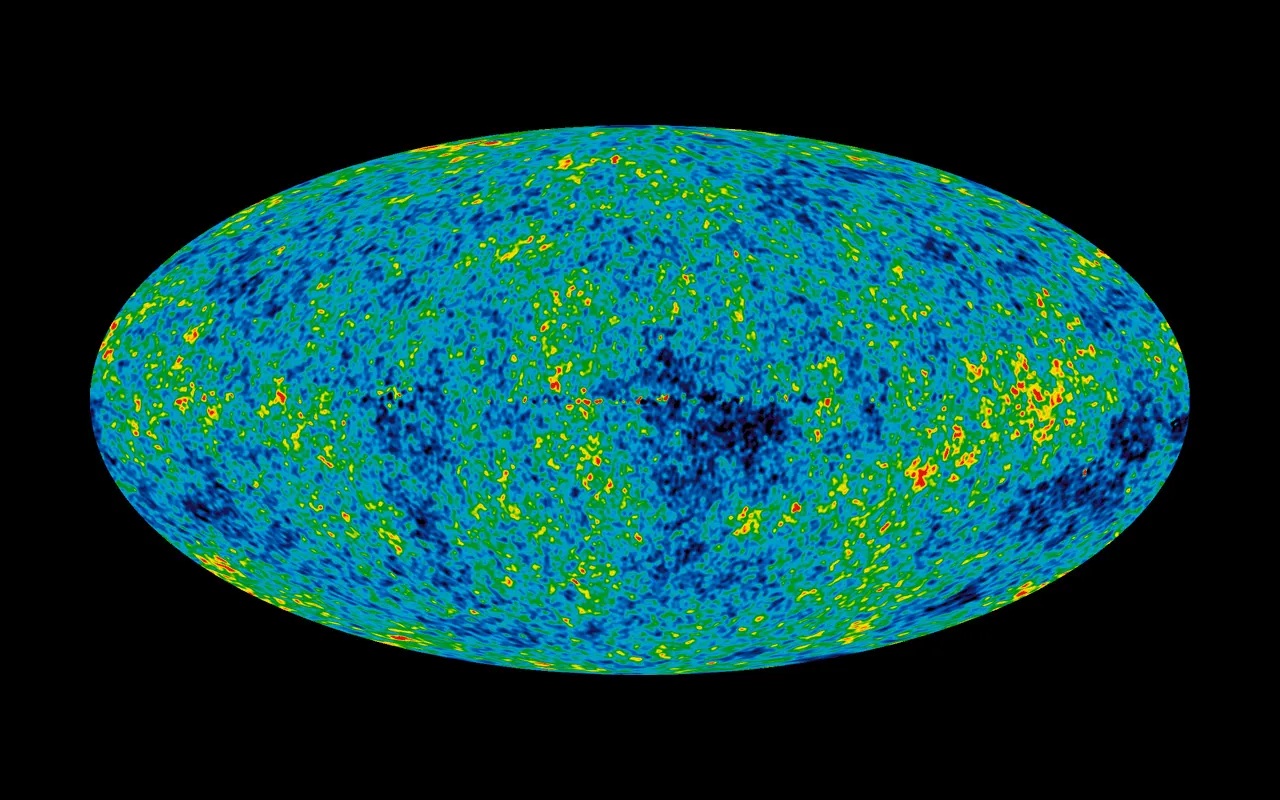
Copyright afbeelding: NASA's WMAP

Uit de analyse van dergelijke beelden heeft men kunnen afleiden dat ons heelal een vlak heelal zou zijn met een gemiddelde dichtheid die gelijk is aan 5 atomen waterstof per kubieke meter, of anders uitgedrukt 10^-23 gram per kubieke meter. Men noemt dit de 'kritische massa'. Maar deze waarde klopt op het eerste gezicht niet met de waargenomen realiteit. De gemiddelde waarde van de massa-energie in het heelal blijkt amper 5% te bedragen van de voornoemde kritische waarde. Waar blijft dan de resterende massa?

In 1933 ontdekte de Zwitserse natuurkundige Fritz Zwicky (1898-1974) dat er nog een ongekend 'iets' aanwezig moet zijn in het heelal. Hij ontdekte dit uit berekeningen van de rotatiesnelheid van sterrenstelsels in de Coma-cluster. De sterrenstelsels bleken een veel te grote rotatiesnelheid te hebben. Om deze rotatiesnelheid te kunnen verklaren moest er nog een andere soort materie aanwezig zijn, zo niet zouden dergelijke sterrenstelsels door het snelle draaien uit mekaar vallen. Men gaf die ongekende materie de naam 'donkere materie'. Het gaat alleszins om een niet te verwaarlozen hoeveelheid, want ze zou ongeveer een kwart bedragen van de kritische dichtheid.

Naar de aard van die donkere materie werd en wordt koortsachtig gezocht, en het is vandaag nog steeds een grote vraag in de astronomie. De meest ingewikkelde wiskundige symmetrieberekeningen hebben tot nu toe geen bevredigend resultaat opgeleverd.

Het bestaan van donkere materie werd nog kracht bijgezet door de ontdekking van zwaartekrachtslenzen. Een dergelijke lens is een gevolg van de relativiteitstheorie die ons aangetoond heeft dat de ruimte gekromd wordt door een massa. Via ingewikkelde berekeningen is men erin geslaagd om uit de graad van de kromming van de ruimte rond sterrenclusters de massa van die clusters te meten. In de figuur hieronder wordt getoond hoe het licht van een melkwegstelsel door een tussenliggende cluster sterrenstelsels afgebogen wordt voor een waarnemer op Aarde. Aan de hand van de kromming kan men de massa van de cluster bepalen. 

Copyright afbeelding: ESA Gravitational lensing

Naast het hypothetische bestaan van donkere materie werd het sterrenkundig onderzoek vervolgens geconfronteerd met een tweede belangrijk probleem: in 1998 ontdekten astronomen Saul Perlmutter, Brian Schmidt en Adam Riess dat het heelal de laatste miljarden jaren versnellend aan het uitdijen is. Om dit te ontdekken moesten ze voor verschillende sterrenstelsels over twee parameters beschikken, hun afstand en hun verwijderingssnelheid. 

De verwijderingssnelheid van sterrenstelsels kan men bepalen uit het spectrum. De afstand meten tot zeer ver gelegen sterrenstelsels was een meer delicate aangelegenheid. Hiervoor maakten ze gebruik van supernovae van het type SNIa. Uit de afstand tot die sterrenstelsels kan men vervolgens, na deling door de lichtsnelheid, weten hoever men in het verleden van het heelal terugkijkt. 

Perlmutter en zijn collega's kwamen in hun studie tot het besluit dat het heelal sinds enkele miljarden jaren aan een versnelde expansie toe is. Een verklaring voor die versnelde expansie heeft men niet. Men kan ze maar verklaren door te veronderstellen dat er in het heelal een afstotende energie aanwezig is waarvan de ware aard niet gekend is. Men noemt deze energie 'donkere energie'. En die zou ongeveer 70% bedragen van de kritische massa van het heelal.

Het is deze energie die Einstein verplicht heeft om aan zijn oorspronkelijke formule die het heelal beschrijft nog een bijkomende term toe te voegen, de kosmologische constante Λ.  

Als we de hypothetische donkere energie en donkere materie in rekening brengen blijkt wel de kritische massa van 5 atomen waterstof per kubieke meter bereikt te zijn.

Copyright afbeelding: ESA Cosmic energy budget

Tekst: Emile Beyens, november 2025